公式及图片正常显示的精美排版版请移步http://lanbing510.info/2015/11/17/Master-Reinforcement-Learning-MDP.html

写在前面

---

现有的机器学习算法根据模型的学习过程大致可以分为四类：监督式学习，无监督式学习，半监督式学习和增强学习。

① 监督式学习：从标记好的训练数据中进行模型的训练，常用来做分类和回归，例如逻辑回归、反向神经网络；

② 无监督式学习：根据数据的特征直接对数据的结构和数值进行归纳，常用来做聚类，例如周知的K-均值，谱聚类；

③ 半监督式学习：根据部分标记的和部分没有标记的训练数据进行模型的学习，常用来做回归和分类；

④ 增强式学习：作为今天要讨论的主角，是机器学习中最酷的分支之一，其通过不断的试错、反馈进行学习，常用来做序列决策或者控制问题，算法例子有Q-Learning、TD-Learning（Tempora Difference Learning）。

增强学习和人类学习的机制非常相近，在实际应用中也有这很Cool的表现，如直升机自动飞行、各种通过增强学习实现的打败人类最强选手的棋牌博弈机器，包括最近非常火的DeepMind将深度学习和增强学习融合实现的玩Atari游戏的超强程序。下面将结合一个实例，从增强学习的数学本质——马尔科夫决策过程进行阐述。

一个栗子

---

下面是摘自《人工智能：一种现代方法》中的一个例子：

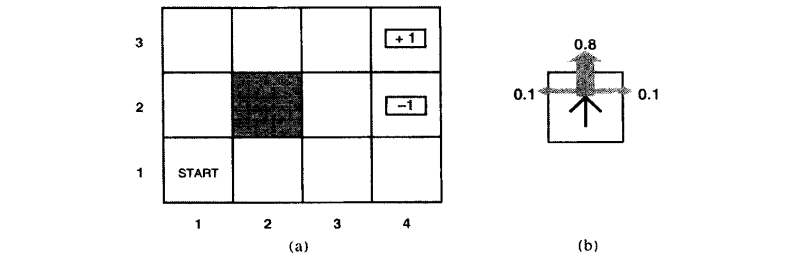
假设一个智能体处于下图（a）中所示的4x3的环境中。从初始状态开始，它需要每个时间选择一个行动（上、下、左、右）。在智能体到达标有+1或-1的目标状态时与环境的交互终止。如果环境是确定的，很容易得到一个解:[上，上，右，右，右]。可惜智能体的行动不是可靠的（类似现实中对机器人的控制不可能完全精确），环境不一定沿这个解发展。下图（b）是一个环境转移模型的示意，每一步行动以0.8的概率达到预期，0.2的概率会垂直于运动方向移动，撞到（a）图中黑色模块后会无法移动。两个终止状态分别有+1和-1的回报，其他状态有-0.4的回报。现在智能体要解决的是通过增强学习（不断的试错、反馈、学习）找到最优的策略（得到最大的回报）。

上述问题可以看作为一个马尔科夫决策过程，最终的目标是通过一步步决策使整体的回报函数期望最优。下面介绍马尔科夫决策过程。

马尔科夫决策过程

---

一个马尔科夫决策过程（Markov Decision Processes, MDP）有一个五个关键元素组成 {S,A,{Psa},γ,R} <script type="math/tex" id="MathJax-Element-1">\{S,A,\{P_{sa}\},\gamma,R\}</script>,其中：

S <script type="math/tex" id="MathJax-Element-2">S</script>：表示状态集合，例如上例中4x3的每个环境{(i,j)|i=1,2,3,4,j=1,2,3}<script type="math/tex" id="MathJax-Element-3">\{(i,j)|i=1,2,3,4,j=1,2,3\}</script>。自动直升机系统中的所有可能的位置、方向等。

A <script type="math/tex" id="MathJax-Element-4">A</script>：表示一组动作集合，例如上例中的（上、下、左、右），自动直升机系统中的让飞机向前，向后等。

Psa<script type="math/tex" id="MathJax-Element-5">P_{sa}</script>：状态转移概率，表示在当前 s∈S <script type="math/tex" id="MathJax-Element-6">s \in S</script>状态下，通过执行动作 a∈A <script type="math/tex" id="MathJax-Element-7">a \in A</script>后转移到其他状态的概率分布。例如上例中， P(1,1)上 <script type="math/tex" id="MathJax-Element-8">P_{(1,1) 上}</script>表示智能体在状态(1,1)执行向上的动作后转移到状态(1,2)，(2,1)的概率分布。

γ∈[0,1) <script type="math/tex" id="MathJax-Element-9">\gamma \in [0,1)</script>：阻尼系数，表示的是随着时间的推移回报率的折扣。

R:S×A↦R <script type="math/tex" id="MathJax-Element-10">R:S \times A \mapsto \mathbb{R}</script>：回报函数，有时回报函数是只与 S <script type="math/tex" id="MathJax-Element-11">S</script>有关的函数，R<script type="math/tex" id="MathJax-Element-12">R</script>重写为 R:S↦R <script type="math/tex" id="MathJax-Element-13">R:S \mapsto \mathbb{R}</script>。相当于上例中对每个状态上赋予的回报值。

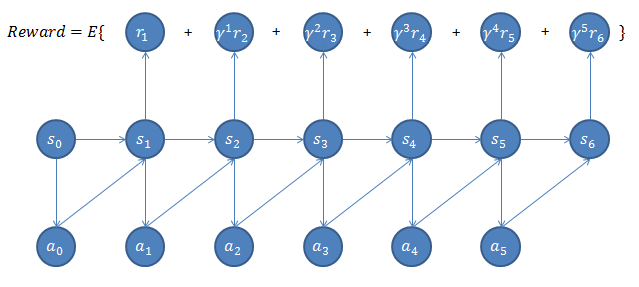
MDP的动态过程如下：智能体在状态 s0 <script type="math/tex" id="MathJax-Element-14">s_{0}</script>选择某个动作 a0∈A <script type="math/tex" id="MathJax-Element-15">a_{0} \in A</script>，智能体根据概率 Ps0a0 <script type="math/tex" id="MathJax-Element-16">P_{s_{0}a_{0}}</script>转移到状态 s1 <script type="math/tex" id="MathJax-Element-17">s_{1}</script>，然后执行动作 a1 <script type="math/tex" id="MathJax-Element-18">a_{1}</script>，…如此下去我们可以得到这样的过程：

<script type="math/tex; mode=display" id="MathJax-Element-19">s_{0} \stackrel{a_{0}}{\longrightarrow} s_{1} \stackrel{a_{1}}{\longrightarrow} s_{2} \stackrel{a_{2}}{\longrightarrow} s_{3} \stackrel{a_{3}}{\longrightarrow} ···</script>

经过上面的转移路径，我们可以得到相应的回报函数和如下：

<script type="math/tex; mode=display" id="MathJax-Element-20">R(s_{0},a_{0})+\gamma R(s_{1},a_{1})+\gamma^{2}R(s_{2},a_{2})+···</script>

如果回报函数 R <script type="math/tex" id="MathJax-Element-21">R</script>只与S<script type="math/tex" id="MathJax-Element-22">S</script>有关，我们上式可重新写作

<script type="math/tex; mode=display" id="MathJax-Element-23">R(s_{0})+\gamma R(s_{1})+\gamma^{2}R(s_{2})+···</script>

我们的目标是选择一组最佳的动作，使得全部的回报加权和期望最大：

<script type="math/tex; mode=display" id="MathJax-Element-136">Reward=E[R(s_{0})+\gamma R(s_{1})+\gamma^{2}R(s_{2})+···]</script>

从上式可以发现，在t时刻的回报值是被打了 γt <script type="math/tex" id="MathJax-Element-137">\gamma^{t}</script>倍折扣的，注意到 γ<1 <script type="math/tex" id="MathJax-Element-138">\gamma < 1</script>，则越靠后的状态对回报和影响越小，为了得到最大期望回报，智能体将会尽量最先拿最大回报。

下图是上述内容的一个直观示意

下一部分将对上述过程进行进一步数学表示，以方便求解。

进一步数学表示

---

首先我们来定义策略，一个策略 π <script type="math/tex" id="MathJax-Element-27">\pi</script>就是一个从状态到动作的映射函数 π:S↦A <script type="math/tex" id="MathJax-Element-28">\pi:S \mapsto A</script>。也就是，给定了当前状态 s <script type="math/tex" id="MathJax-Element-29">s</script>，根据策略π<script type="math/tex" id="MathJax-Element-30">\pi</script>，也就确定了下一步应该执行的动作 a=π(s) <script type="math/tex" id="MathJax-Element-31">a=\pi(s)</script>。

为每一个策略 π <script type="math/tex" id="MathJax-Element-32">\pi</script>我们顶一个相应的值函数（Value Function）

<script type="math/tex; mode=display" id="MathJax-Element-33">V^{\pi}(s)=E[R(s_{0})+\gamma R(s_{1})+\gamma^{2}R(s_{2})+···|s_{0}=s,\pi]</script>

即给定初始状态 s0 <script type="math/tex" id="MathJax-Element-34">s_{0}</script>和策略 π <script type="math/tex" id="MathJax-Element-35">\pi</script>后的累积折扣回报期望（Expected Sum Of Discounted Rewards）。

对于一个固定的策略，它的值函数 Vπ <script type="math/tex" id="MathJax-Element-36">V^{\pi}</script>满足贝尔曼等式（Bellman Equations）：

<script type="math/tex; mode=display" id="MathJax-Element-37">V^{\pi}(s)=R(s)+\gamma \sum_{s' \in S}P_{s\pi(s)}(s')V^{\pi}(s')</script>

其中 s′ <script type="math/tex" id="MathJax-Element-38">s'</script>表示状态 s <script type="math/tex" id="MathJax-Element-39">s</script>执行动作π(s)<script type="math/tex" id="MathJax-Element-40">\pi(s)</script>后的下一个可能状态，其服从 Psπ(s) <script type="math/tex" id="MathJax-Element-41">P_{s\pi(s)}</script>分布。上式由两部分构成：即时回报 R(s) <script type="math/tex" id="MathJax-Element-42">R(s)</script>及未来累积折扣回报期望 Es′∼Psπ(s)[Vπ(s′)] <script type="math/tex" id="MathJax-Element-43">E_{s' \sim P_{s\pi(s)}}[V^{\pi}(s')]</script>。

利用贝尔曼等式能够有效的解出 Vπ <script type="math/tex" id="MathJax-Element-44">V^{\pi}</script>（给定的策略 π <script type="math/tex" id="MathJax-Element-45">\pi</script>的回报值）。尤其，对于一个有限状态的MDP（ |S|<∞ <script type="math/tex" id="MathJax-Element-46">|S| < \infty</script>），对每一个状态 s <script type="math/tex" id="MathJax-Element-47">s</script>我们都能写出这样的等式Vπ(s)<script type="math/tex" id="MathJax-Element-48">V^{\pi}(s)</script>，求解变为了解一个 |S| <script type="math/tex" id="MathJax-Element-49">|S|</script>个方程， |S| <script type="math/tex" id="MathJax-Element-50">|S|</script>个未知数的线性方程组。

当然，我们求解 Vπ <script type="math/tex" id="MathJax-Element-51">V^{\pi}</script>的目的是为找到一个当前状态 s <script type="math/tex" id="MathJax-Element-52">s</script>下最优的行动策略π<script type="math/tex" id="MathJax-Element-53">\pi</script>服务的（最优的策略下得到最优的值函数）。定义最优的值函数为：

<script type="math/tex; mode=display" id="MathJax-Element-54">V^{*}(s)=\max_{\pi}V^{\pi}(s)</script>

其贝尔曼等式的形式为：

<script type="math/tex; mode=display" id="MathJax-Element-55">V^{*}(s)=R(s)+\max_{a \in A}\gamma\sum_{s' \in S}P_{sa}(s')V^{*}(s')</script>

也可表示为增强学习中的Q函数形式：

<script type="math/tex; mode=display" id="MathJax-Element-56">V^{*}(s)=\max_{a}Q(s,a)</script>

其中 Q(s,a)≡R(S)+γPsa(s′)V∗(s′) <script type="math/tex" id="MathJax-Element-57">Q(s,a) \equiv R(S)+\gamma P_{sa}(s')V^{*}(s')</script>，表示在 s <script type="math/tex" id="MathJax-Element-58">s</script>状态下执行动作a<script type="math/tex" id="MathJax-Element-59">a</script>作为第一个动作时的最大累计折扣回报。

对应最优值函数的最优的策略为：

<script type="math/tex; mode=display" id="MathJax-Element-60">\pi^{*}(s)=arg\max_{a \in A}\sum_{s' \in S}P_{sa}(s')V^{*}(s')</script>

需要注意的是， π∗ <script type="math/tex" id="MathJax-Element-61">\pi^{*}</script>有一个有趣的特性，即 π∗ <script type="math/tex" id="MathJax-Element-62">\pi^{*}</script>是针对的是所有的状态 s <script type="math/tex" id="MathJax-Element-63">s</script>的，确定了每一个状态s<script type="math/tex" id="MathJax-Element-64">s</script>的下一个动作 a <script type="math/tex" id="MathJax-Element-65">a</script>，不管初始状态是哪一个状态，通过策略π∗<script type="math/tex" id="MathJax-Element-66">\pi^{*}</script>都会取得最大回报。

现在我们有了优化目标的数学表达（最优值函数，最优策略），下一部分讨论两种求解方法（针对有限状态、有限动作的MDP）。

值迭代方法和策略迭代方法

---

值迭代方法

算法步骤：

1 讲每一个状态 s <script type="math/tex" id="MathJax-Element-67">s</script>的值函数V(s)<script type="math/tex" id="MathJax-Element-68">V(s)</script>初始化为0

2 循环直至收敛{

  对于每一个状态 s <script type="math/tex" id="MathJax-Element-69">s</script>，对V(s)<script type="math/tex" id="MathJax-Element-70">V(s)</script>做更新

  V(s):=R(s)+maxa∈Aγ∑s′V(s′) <script type="math/tex" id="MathJax-Element-71">V(s):=R(s)+\max_{a \in A}\gamma\sum_{s'}V(s')</script>

}

值迭代方法里面的内循环又有两种策略：同步迭代，异步迭代。同步迭代就是得到 V(s) <script type="math/tex" id="MathJax-Element-72">V(s)</script>后不立即更新，等所有的状态 s <script type="math/tex" id="MathJax-Element-73">s</script>的V(s)<script type="math/tex" id="MathJax-Element-74">V(s)</script>都完成计算后统一更新。异步迭代就是对每个状态 s <script type="math/tex" id="MathJax-Element-75">s</script>得到新的V(s)<script type="math/tex" id="MathJax-Element-76">V(s)</script>后立即更新。两种都会使得 V(s) <script type="math/tex" id="MathJax-Element-77">V(s)</script>收敛于 V∗(s) <script type="math/tex" id="MathJax-Element-78">V^{*}(s)</script>。求得最优的 V∗(s) <script type="math/tex" id="MathJax-Element-79">V^{*}(s)</script>后，可使用公式 π∗(s)=argmaxa∈A∑s′∈SPsa(s′)V∗(s′) <script type="math/tex" id="MathJax-Element-80">\pi^{*}(s)=arg\max_{a \in A}\sum_{s' \in S}P_{sa}(s')V^{*}(s')</script>来求出相应的最优策略 π∗ <script type="math/tex" id="MathJax-Element-81">\pi^{*}</script>。

策略迭代方法

于值迭代方法不同，策略迭代法之间关注 π <script type="math/tex" id="MathJax-Element-82">\pi</script>，使 π <script type="math/tex" id="MathJax-Element-83">\pi</script>收敛到 π∗ <script type="math/tex" id="MathJax-Element-84">\pi^{*}</script>。

算法步骤：

1 随机初始化话一个 S <script type="math/tex" id="MathJax-Element-85">S</script>到A<script type="math/tex" id="MathJax-Element-86">A</script>的映射 π <script type="math/tex" id="MathJax-Element-87">\pi</script>

2 循环直至收敛{

  2.1 令 V:=Vπ <script type="math/tex" id="MathJax-Element-88">V:=V^{\pi}</script>

  2.2 对每一个状态s,对 π(s) <script type="math/tex" id="MathJax-Element-89">\pi(s)</script>做更新

  π(s):=argmaxa∈A∑s′Psa(s′)V(s′) <script type="math/tex" id="MathJax-Element-90">\pi(s):=arg\max_{a \in A}\sum_{s'}P_{sa}(s')V(s')</script>

}

其中2.1步即为上述对于一个给定策略 π <script type="math/tex" id="MathJax-Element-91">\pi</script>利用贝尔曼等式求解 Vπ <script type="math/tex" id="MathJax-Element-92">V^{\pi}</script>的过程（求解 |S| <script type="math/tex" id="MathJax-Element-93">|S|</script>个方程， |S| <script type="math/tex" id="MathJax-Element-94">|S|</script>个未知数的线性方程组）。

2.2是根据2.1步的结果，挑选出当前状态 s <script type="math/tex" id="MathJax-Element-95">s</script>下最优的动作a<script type="math/tex" id="MathJax-Element-96">a</script>来更新 π(s) <script type="math/tex" id="MathJax-Element-97">\pi(s)</script>。

两者比较

对于规模较小的MDP，策略迭代一般能够更快的收敛；但对于规模较大的MDP（状态多），值迭代更容易些（没有线性方程组的计算）。

MDP中的参数估计

---

到目前为止，我们讨论的MDP和MDP求解算法都是在已知状态转移概率 Psa <script type="math/tex" id="MathJax-Element-98">P_{sa}</script>和回报函数 R(s) <script type="math/tex" id="MathJax-Element-99">R(s)</script>的。在许多实际问题中，状态转移概率和回报函数不能显式的得到，本部分讲如何从数据中估计这些参数（通常 S,A,γ <script type="math/tex" id="MathJax-Element-100">S,A,\gamma</script>是已知的）。

假设我们已知很多条状态转移路径如下：

<script type="math/tex; mode=display" id="MathJax-Element-101">s_{0}^{(1)} \stackrel{a_{0}^{(1)}}{\longrightarrow} s_{1}^{(1)} \stackrel{a_{1}^{(1)}}{\longrightarrow} s_{2}^{(1)} \stackrel{a_{2}^{(1)}}{\longrightarrow} s_{3}^{(1)} \stackrel{a_{3}^{(1)}}{\longrightarrow} ···</script>

<script type="math/tex; mode=display" id="MathJax-Element-102">s_{0}^{(2)} \stackrel{a_{0}^{(2)}}{\longrightarrow} s_{1}^{(2)} \stackrel{a_{1}^{(2)}}{\longrightarrow} s_{2}^{(2)} \stackrel{a_{2}^{(2)}}{\longrightarrow} s_{3}^{(2)} \stackrel{a_{3}^{(2)}}{\longrightarrow} ···</script>

<script type="math/tex; mode=display" id="MathJax-Element-103">···</script>

其中 s(j)i <script type="math/tex" id="MathJax-Element-104">s_{i}^{(j)}</script>是 i <script type="math/tex" id="MathJax-Element-105">i</script>时刻第j<script type="math/tex" id="MathJax-Element-106">j</script>条转移路径对应的状态， aji <script type="math/tex" id="MathJax-Element-107">a_{i}^{j}</script>是 sji <script type="math/tex" id="MathJax-Element-108">s_{i}^{j}</script>状态要执行的动作。每条转移路径中的状态数都是有限的，在实际操作中每个转移路径要么进入终结状态，要不达到规定的步数后终结。

当我们获得了很多类似上面的转移路径后（样本），我们可以用最大似然估计来估计状态转移概率。

<script type="math/tex; mode=display" id="MathJax-Element-109">P_{sa}(s')=\frac{\#times\ took\ we\ action\ a\ in\ state\ s\ and\ got\ to\ s'}{\#times\ we\ took\ action\ a\ in\ state\ s}</script>

上式分子表示在状态 s <script type="math/tex" id="MathJax-Element-110">s</script>通过执行动作a<script type="math/tex" id="MathJax-Element-111">a</script>后到达状态 s′ <script type="math/tex" id="MathJax-Element-112">s'</script>的次数，分母表示在状态 s <script type="math/tex" id="MathJax-Element-113">s</script>我们执行动作的次数。为避免分母为0的情况，当分母为0使，令Psa(s′)=1|S|<script type="math/tex" id="MathJax-Element-114">P_{sa}(s')=\frac{1}{|S|}</script>。

对于未知的回报函数，我们令 R(s) <script type="math/tex" id="MathJax-Element-115">R(s)</script>为在状态 s <script type="math/tex" id="MathJax-Element-116">s</script>下观察到的回报均值。

得到状态转移概率和回报函数的估值后，就简化为了前面部分讲述的问题，用第三部分将的值迭代或者策略迭代方法即可解决。例如我们将值迭代和参数估计结合到一块：

算法流程如下：

1 随机初始化话一个S<script type="math/tex" id="MathJax-Element-117">S</script>到 A <script type="math/tex" id="MathJax-Element-118">A</script>的映射π<script type="math/tex" id="MathJax-Element-119">\pi</script>

2 循环直至收敛{

  2.1 在MDP中执行策略 π <script type="math/tex" id="MathJax-Element-120">\pi</script>一定次数

  2.2 通过2.1得到的样本估计 Psa <script type="math/tex" id="MathJax-Element-121">P_{sa}</script>（和 R <script type="math/tex" id="MathJax-Element-122">R</script>，需要的话）

  2.3 使用上一节提到的值迭代方法和估计得到的参数来更新V<script type="math/tex" id="MathJax-Element-123">V</script>

  2.4 对于得到的 V <script type="math/tex" id="MathJax-Element-124">V</script>更新得到更优的策略π<script type="math/tex" id="MathJax-Element-125">\pi</script>

}

其中2.3步，是一个循环迭代的过程。上一节中我们通过将 V <script type="math/tex" id="MathJax-Element-126">V</script>初始化为0然后进行迭代，当嵌套上述过程中后，如果每次都将V<script type="math/tex" id="MathJax-Element-127">V</script>初始化为0然后迭代更新，速度回很慢。一个加速的方法是将 V <script type="math/tex" id="MathJax-Element-128">V</script>初始化我上次大循环中得到的V<script type="math/tex" id="MathJax-Element-129">V</script>。

小结

---

至此我们讨论完了增强学习的数学本质————马尔科夫决策过程（MDP）的数学表示及求解过程（这里的MDP是非确定的MDP，即状态转移函数和回报函数是有概率的,，对于确定性的，求解会更简单些，感兴趣可参考[3]最后一章：增强学习）。全文很大部分是对Andrew Ng讲义[1]的翻译，加上了部分自己的理解。推荐大家根据参考文献进行进一步理解和学习。

参考文献

---

[1] 机器学习公开课-讲义-马尔科夫决策过程.Andrew Ng

[2] 机器学习公开课-视频-马尔科夫决策过程.Andrew Ng

[3] 人工智能：一种现代方法

[4] 机器学习.Tom M.Mitchell

[5] 看DeepMind如何用Reinforcement learning玩游戏