一、极限学习机的概念

　　极限学习机(Extreme Learning Machine) ELM，是由黄广斌提出来的求解单隐层神经网络的算法。
　　ELM最大的特点是对于传统的神经网络，尤其是单隐层前馈神经网络(SLFNs)，在保证学习精度的前提下比传统的学习算法速度更快。

二、极限学习机的原理

　　ELM是一种新型的快速学习算法，对于单隐层神经网络，ELM可以随机初始化输入权重和偏置并得到相应的输出权重。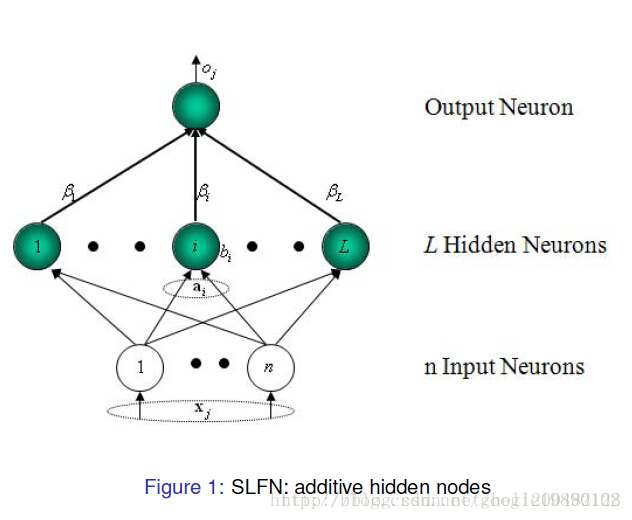

　　　　　　　　　　(选自黄广斌老师的PPT)
　　对于一个单隐层神经网络(见Figure 1)，假设有 Ｎ <script type="math/tex" id="MathJax-Element-40">Ｎ</script>个任意的样本(Xi,ti<script type="math/tex" id="MathJax-Element-41">X_i,t_i</script>)，其中 Xi=[xi1,xi2,...,xin]T∈Rn <script type="math/tex" id="MathJax-Element-42">X_i = [x_{i1}, x_{i2}, ..., x_{in}]^T \in R^n</script>， ti=[ti1,ti2,...,tim]T∈Rm <script type="math/tex" id="MathJax-Element-43">t_i = [t_{i1}, t_{i2}, ..., t_{im}]^T \in R^m</script>。对于一个有 L <script type="math/tex" id="MathJax-Element-44">L</script>个隐层节点的单隐层神经网络可以表示为

<script type="math/tex; mode=display" id="MathJax-Element-45">\sum_{i=1}^L \beta_ig(W_i · X_j + b_i) = o_j, j = 1, ..., N</script>
　　其中， g(x) <script type="math/tex" id="MathJax-Element-46">g(x)</script>为激活函数， Wi=[wi1,wi2,...,win]T <script type="math/tex" id="MathJax-Element-47">W_i = [w_{i1}, w_{i2}, ..., w_{in}]^T</script>为输入权重， βi <script type="math/tex" id="MathJax-Element-48">\beta_i</script>输出权重， bi <script type="math/tex" id="MathJax-Element-49">b_i</script>是第 i <script type="math/tex" id="MathJax-Element-50">i</script>个隐层单元的偏置。Wi⋅Xj<script type="math/tex" id="MathJax-Element-51">W_i · X_j</script>表示 Wj <script type="math/tex" id="MathJax-Element-52">W_j</script>和 Xj <script type="math/tex" id="MathJax-Element-53">X_j</script>的内积。
　　单隐层神经网络学习的目标是使得输出的误差最小，可以表示为

<script type="math/tex; mode=display" id="MathJax-Element-54">\sum_{j=1}^N ||o_j - t_j|| = 0</script>
　　即存在 βi <script type="math/tex" id="MathJax-Element-55">\beta_i</script>， Wi <script type="math/tex" id="MathJax-Element-56">W_i</script>和 bi <script type="math/tex" id="MathJax-Element-57">b_i</script>，使得 <script type="math/tex; mode=display" id="MathJax-Element-58">\sum_{i=1}^L \beta_ig(W_i · X_j + b_i) = t_j, j = 1, ..., N</script>
　　可以矩阵表示为 <script type="math/tex; mode=display" id="MathJax-Element-59">H\beta = T</script>
　　其中， H <script type="math/tex" id="MathJax-Element-60">H</script>是隐层节点的输出，β<script type="math/tex" id="MathJax-Element-61">\beta</script>为输出权重， T <script type="math/tex" id="MathJax-Element-62">T</script>为期望输出。 <script type="math/tex; mode=display" id="MathJax-Element-63">H(W_1, ..., W_L, b_1, ..., b_L, X_1, ..., X_L) = \left[\begin{matrix}g(W_1 · X_1 + b_1)\quad \cdots\quad g(W_L · X_1 + b_L)\\\vdots\qquad \cdots\qquad \vdots\\g(W_1 · X_N + b_1)\quad \cdots\quad g(W_L · X_N + b_L)\end{matrix}\right]_{N×L}</script> <script type="math/tex; mode=display" id="MathJax-Element-64">\beta = \left[\begin{matrix}\beta_1^T\\\vdots\\\beta_L^T\end{matrix}\right]_{L×m}, T = \left[\begin{matrix}T_1^T\\\vdots\\T_L^T\end{matrix}\right]_{L×m}</script>
　　为了能够训练单隐层神经网络，我们希望得到 W^i <script type="math/tex" id="MathJax-Element-65">\hat{W}_i</script>， b^i <script type="math/tex" id="MathJax-Element-66">\hat{b}_i</script>和 β^i <script type="math/tex" id="MathJax-Element-67">\hat{\beta}_i</script>，使得 <script type="math/tex; mode=display" id="MathJax-Element-68">||H(\hat{W}_i, \hat{b}_i)\hat{\beta}_i - T|| = \min_{W,b,\beta}||H(W_i, b_i)\beta_i - T||</script>
　　其中， i=1,...,L <script type="math/tex" id="MathJax-Element-69">i = 1, ..., L</script>，这等价于最小化损失函数 <script type="math/tex; mode=display" id="MathJax-Element-70">E = \sum_{j=1}^N(\sum_{i=1}^L \beta_ig(W_i · X_j + b_i) - t_j)^2</script>
　　传统的一些基于梯度下降法的算法，可以用来求解这样的问题，但是基本的基于梯度的学习算法需要在迭代的过程中调整所有参数。而在ELM算法中, 一旦输入权重 Wi <script type="math/tex" id="MathJax-Element-71">W_i</script>和隐层的偏置 bi <script type="math/tex" id="MathJax-Element-72">b_i</script>被随机确定，隐层的输出矩阵 H <script type="math/tex" id="MathJax-Element-73">H</script>就被唯一确定。训练单隐层神经网络可以转化为求解一个线性系统Hβ=T<script type="math/tex" id="MathJax-Element-74">H\beta = T</script>。并且输出权重 β <script type="math/tex" id="MathJax-Element-75">\beta</script>可以被确定 <script type="math/tex; mode=display" id="MathJax-Element-76">\hat\beta = H^+T</script>
　　其中，是矩阵的Moore-Penrose广义逆。且可证明求得的解的范数是最小的并且唯一。

三 实验

　　我们使用《简单易学的机器学习算法——Logistic回归》中的实验数据。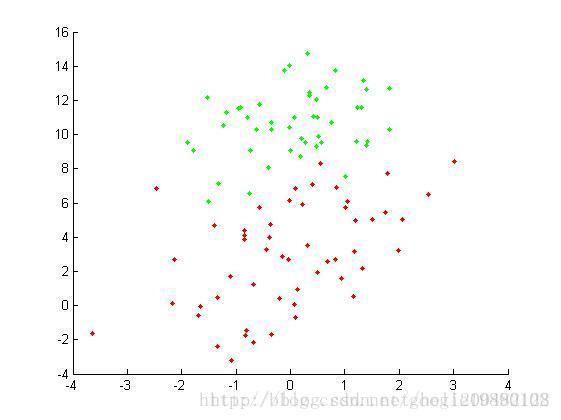

　　　　　　　　　　　　原始数据集
　　我们采用统计错误率的方式来评价实验的效果，其中错误率公式为：

<script type="math/tex; mode=display" id="MathJax-Element-77">errorRate = \frac{NumError}{NumAll}</script>

　　对于这样一个简单的问题， errorRate=0 <script type="math/tex" id="MathJax-Element-78">errorRate = 0</script>。
　　MATLAB代码
　　主程序

%% 主函数，二分类问题  

%导入数据集  
A = load('testSet.txt');  

data = A(:,1:2);%特征  
label = A(:,3);%标签  

[N,n] = size(data);  

L = 100;%隐层节点个数  
m = 2;%要分的类别数  

%--初始化权重和偏置矩阵  
W = rand(n,L)*2-1;  
b_1 = rand(1,L);  
ind = ones(N,1);  
b = b_1(ind,:);%扩充成N*L的矩阵  

tempH = data*W+b;  
H = g(tempH);%得到H  

%对输出做处理  
temp_T=zeros(N,m);  
for i = 1:N  
    if label(i,:) == 0  
        temp_T(i,1) = 1;  
    else   
        temp_T(i,2) = 1;  
    end      
end  
T = temp_T*2-1;  

outputWeight = pinv(H)*T;  

%--画出图形  
x_1 = data(:,1);    
x_2 = data(:,2);    
hold on    
for i = 1 : N    
    if label(i,:) == 0    
        plot(x_1(i,:),x_2(i,:),'.g');    
    else    
        plot(x_1(i,:),x_2(i,:),'.r');    
    end    
end  

output = H * outputWeight;  
%---计算错误率  
tempCorrect=0;  
for i = 1:N  
    [maxNum,index] = max(output(i,:));  
    index = index-1;  
    if index == label(i,:);  
        tempCorrect = tempCorrect+1;  
    end  
end  

errorRate = 1-tempCorrect./N;  

　　激活函数

function [ H ] = g( X )  
    H = 1 ./ (1 + exp(-X));  
end  

---

黄老师提供的极限学习机的代码：http://www.ntu.edu.sg/home/egbhuang/elm_codes.html